BIOT Y SAVART

Campo magnético creado por una corriente eléctrica cualquiera

Jean Baptiste Biot (1774-1862) y Félix Savart (1791-1841) establecierón poco después de que Oersted (1777-1851) divulgara su experiencia, que al igual que una carga origina un campo eléctrico o una masa un campo gravitatorio, un elemento de corriente genera un campo magnético. Un elemento de corriente es la intensidad que fluye por una porción tangente al hilo conductor de longitud infinitesimal y cuyo sentido es el de la corriente eléctrica (dl→). Su expresión viene dada por I⋅dl→

I⋅dl→=dqdt⋅dl→=dq⋅dl→dt=dq⋅v→ ⇒I⋅dl→=dq⋅v→

La ley de Biot y Savart establece que el campo magnético producido por una corriente cualquiera en un punto P viene determinado por la siguiente expresión:

B→=μ0⋅I4⋅π∫ldl→×u→rr2

donde:

• B→ es la intensidad del campo magnético creado en un punto P.
• μ0 es la permeabilidad magnética del vacío. En el S.I. se mide en m·kg/C2.
• I es la intensidad de corriente que circula por dl→. En el S.I. se mide en Amperios (A).
• dl→ vector en la dirección de la intensidad de corriente. En el S.I. se mide en metros (m).
• u→r es un vector unitario que une el elemento de corriente I⋅dl→ con el punto P donde se mide la intensidad del campo magnético (B→).

Su módulo se puede calcular por medio de la siguiente expresión:

B=μ0⋅I4⋅π∫ldl⋅sin αr2

Si en vez de una corriente eléctrica indefinida disponemos de una corriente en línea recta, el cálculo del campo magnético creado por dicha corriente se simplifica enormemente.

El valor del campo magnético creado por una corriente rectilínea en un punto P se obtiene por medio de la siguiente expresión:

B=μ0⋅I2⋅π⋅R

donde:

• B es el valor del campo magnético en el punto P. Su unidad en el S.I. es el Tesla (T).
• μ0 es la permeabilidad magnética del vacío. En el S.I. se mide en m·kg/C2.
• I es la intensidad de corriente que circula en línea recta. Su unidad en el S.I. es el Amperio (A).
• R es la distancia más corta en línea recta desde P hasta la corriente. Su unidad en el S.I. es el metro (m).

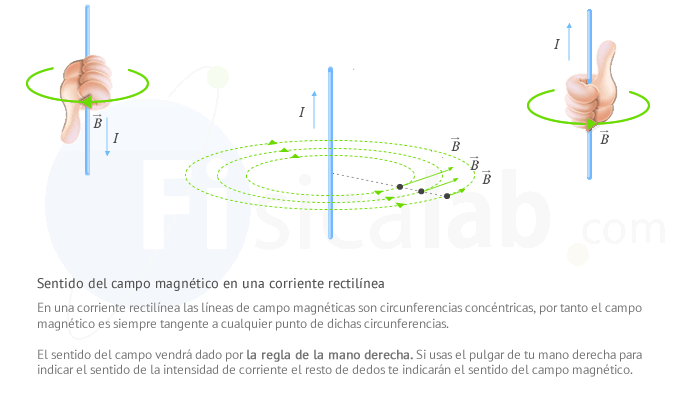
Las líneas de campo creadas por este tipo de corriente son circunferencias concéntricas al conductor y perpendiculares a él. Esto implica que la dirección del campo magnético sea tangente a ellas en cada punto y su sentido venga dado por la regla de la mano derecha. La regla de la mano derecha determina que si usamos el pulgar de dicha mano para indicar el sentido de la intensidad de corriente, el resto de dedos nos indicará el sentido del campo magnético.

Comprobación

Si aplicamos la definición de campo magnético en un punto P creado por una corriente cualquiera, obtenemos que:

B→=μ0⋅I4⋅π∫ldl→×u→rr2

Si observamos, el producto vectorial de dl→ y r→ provocará que B→ tenga la dirección perpendicular a tu pantalla orientado hacia dentro. En este caso el módulo se obtiene por medio de la siguiente expresión:

B=μ0⋅I4⋅π∫l∣∣∣dl→×u→r∣∣∣r2⇒B=μ0⋅I4⋅π∫lI⋅dl⋅sin αr2

Estudiando de forma gráfica que ocurre con un elemento de corriente cualquiera, podemos representar la situación de la siguiente forma:

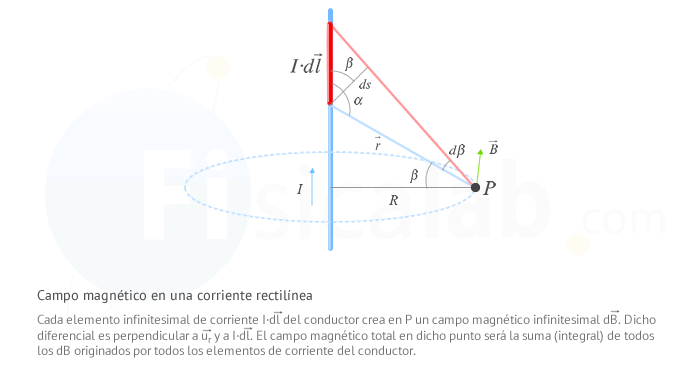
De la figura anterior se pueden deducir las siguientes equivalencias:

sin α = cos βds=r⋅dβdl=dscos βR=r⋅cos β

Por lo que simplificando:

dl⋅sin αr2=dl⋅cos βr2=dsr2=r⋅dβr2=cos β⋅dβR

Aplicando esta expresión al cálculo del módulo del campo magnético, podemos deducir que:

B=μ0⋅I4⋅π⋅∫Ldl⋅sin αr2⇒B=μ0⋅I4⋅π⋅R⋅∫+π/2−π2/cos β⋅dβ ⇒B=μ0⋅I4⋅π⋅R⋅[sin β]+π/2−π/2⇒B=μ0⋅I2⋅π⋅R